K-Mean clustering 算法 非监督学习算法
由此延伸 监督学习和非监督学习的区别
- 监督学习:通过已有的一部分输入数据与输出数据之间的对应关系,生成一个函数,将输入映射到合适的输出,例如分类。 classify 利用之前的训练资料建立模型,并依次模式推测新的实例。
例如朴素贝叶斯 , 有类别标签, 也就是说样例中已经给出了样例的分类 然而聚类样本中没有给定y, 只有特征x。
- 非监督学习:直接对输入数据集进行建模,例如聚类。clustering 不同于监督学习,根据原始的数据,自动从中找出潜在的类别规则。并经测试后,应用到新的案例上去。
K-means is one of the unsupervised learning algorithm
The main idea is to define k centers, one of each cluster.**
k-means(k-均值)算法是一种基于距离的聚类算法,它用质心(Centroid)到属于该质心的点距离这个度量来实现聚类,通常可以用于N维空间中对象。下面,我们以二维空间为例,概要地总结一下k-means聚类算法的一些要点:
由于k-means算法比较简单,对于算法的实现过程,我们概要地描述如下:
1) 随机选择k个初始质心; 2) 如果没有满足聚类算法终止条件,则继续执行步骤3,否则转步骤5; 3) 计算每个非质心点p到k个质心的,将p指派给距离最近的质心; 计算每一个非质心点到其他K个质心点的欧几里得距离(欧几里得距离值越小,代表距离越近,代表相似度越高,这两个点相似度越高,就可以归为一类) 4) 根据上一步的k个质心及其对应的非质心点集,重新计算新的质心点,然后转步骤2; 就平均,得到新的质心, 5) 输出聚类结果,算法可以执行多次,使用散点图比较不同的聚类结果。
Euclidean distance :
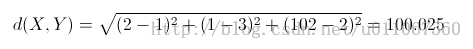
* 除了随机选择的初始质心,后续迭代质心是根据给定的待聚类的集合S中点计算均值得到的,所以质心一般不是S中的点,但是标识的是一簇点的中心。
基本k-means算法,开始需要随机选择指定的k个质心,因为初始k个质心是随机选择的,所以每次执行k-means聚类的结果可能都不相同。如果初始随机选择的质心位置不好,可能造成k-means聚类的结果非常不理想。
计算质心:假设k-means聚类过程中,得到某一个簇的集合Ci={p(x1,y1), p(x2,y2), …,p(xn,yn)},则簇Ci的质心,质心x坐标为(x1+x2+ …+xn)/n,质心y坐标为(y1+y2+ …+yn)/n。
k-means算法的终止条件:质心在每一轮迭代中会发生变化,然后需要重新将非质心点指派给最近的质心而形成新的簇,如果只有很少的一部分点在迭代过程中,还在改变簇(如,更新一次质心,有些点从一个簇移动到另一个簇),那么满足这样一个收敛条件,可以提前结束迭代过程。
k-means算法的框架是:首先随机选择k个初始质心点,然后执行聚类处理迭代,不断更新质心,直到满足算法收敛条件。由于该算法收敛于局部最优,所以多次执行聚类算法,通过比较,选择聚类效果最好的结果作为最终的结果。
k-means算法聚类完成后,没有离群点,所有的点都会被指派到对应的簇中。
计算每一簇中,与簇内其他点距离之和最小的点,作为质心。
优势:
1, Fast , robust , easier to understand
2, Relatively efficient: O(tknd), where n is # objects, k is # clusters, d is # dimension of each object, and t is # iterations. Normally, k, t, d << n.
3, Gives best result when data set are distinct or well separated from each other.
缺点:
1, K-means 对于K 的选择是事先给定的, 也就是说K值的选定是非常难以估计的, 很多时候事先并不知道数据集应该被分成多少个cluster,
2,在 K-means 算法中,首先需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响,一旦初始值选择的不好,可能无法得到有效的聚类结果
3,从 K-means 算法框架可以看出,该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。所以需要对算法的时间复杂度进行分析、改进,提高算法应用范围。